Breadth First Search or BFS for a Graph

Breadth First Traversal (or Search) for a graph is similar to Breadth First Traversal of a tree (See method 2 of this post). The only catch here is, unlike trees, graphs may contain cycles, so we may come to the same node again. To avoid processing a node more than once, we use a boolean visited array. For simplicity, it is assumed that all vertices are reachable from the starting vertex.
For example, in the following graph, we start traversal from vertex 2. When we come to vertex 0, we look for all adjacent vertices of it. 2 is also an adjacent vertex of 0. If we don’t mark visited vertices, then 2 will be processed again and it will become a non-terminating process. A Breadth First Traversal of the following graph is 2, 0, 3, 1.

Following are the implementations of simple Breadth First Traversal from a given source.

The implementation uses adjacency list representation of graphs. STL‘s list container is used to store lists of adjacent nodes and queue of nodes needed for BFS traversal.

// Program to print BFS traversal from a given // source vertex. BFS(int s) traverses vertices  // reachable from s. #include<iostream> #include <list>    using namespace std;    // This class represents a directed graph using // adjacency list representation class Graph {     int V;    // No. of vertices        // Pointer to an array containing adjacency     // lists     list<int> *adj;    public:     Graph(int V);  // Constructor        // function to add an edge to graph     void addEdge(int v, int w);         // prints BFS traversal from a given source s     void BFS(int s);   };    Graph::Graph(int V) {     this->V = V;     adj = new list<int>[V]; }    void Graph::addEdge(int v, int w) {     adj[v].push_back(w); // Add w to v’s list. }    void Graph::BFS(int s) {     // Mark all the vertices as not visited     bool *visited = new bool[V];     for(int i = 0; i < V; i++)         visited[i] = false;        // Create a queue for BFS     list<int> queue;        // Mark the current node as visited and enqueue it     visited[s] = true;     queue.push_back(s);        // 'i' will be used to get all adjacent     // vertices of a vertex     list<int>::iterator i;        while(!queue.empty())     {         // Dequeue a vertex from queue and print it         s = queue.front();         cout << s << " ";         queue.pop_front();            // Get all adjacent vertices of the dequeued         // vertex s. If a adjacent has not been visited,          // then mark it visited and enqueue it         for (i = adj[s].begin(); i != adj[s].end(); ++i)         {             if (!visited[*i])             {                 visited[*i] = true;                 queue.push_back(*i);             }         }     } }    // Driver program to test methods of graph class int main() {     // Create a graph given in the above diagram     Graph g(4);     g.addEdge(0, 1);     g.addEdge(0, 2);     g.addEdge(1, 2);     g.addEdge(2, 0);     g.addEdge(2, 3);     g.addEdge(3, 3);        cout << "Following is Breadth First Traversal "          << "(starting from vertex 2) \n";     g.BFS(2);        return 0; }

Output:

Following is Breadth First Traversal (starting from vertex 2)
2 0 3 1

Illustration :

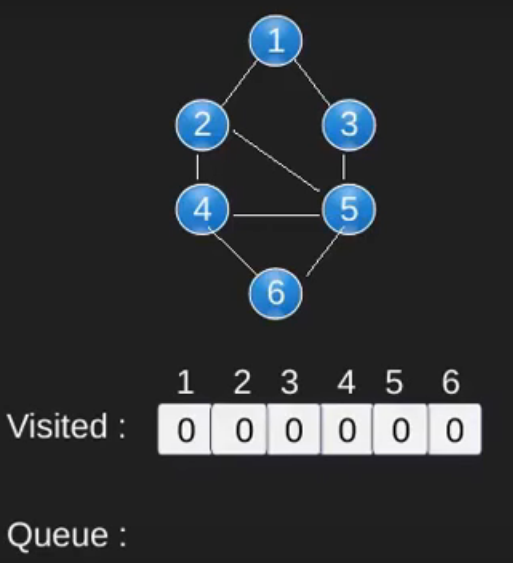
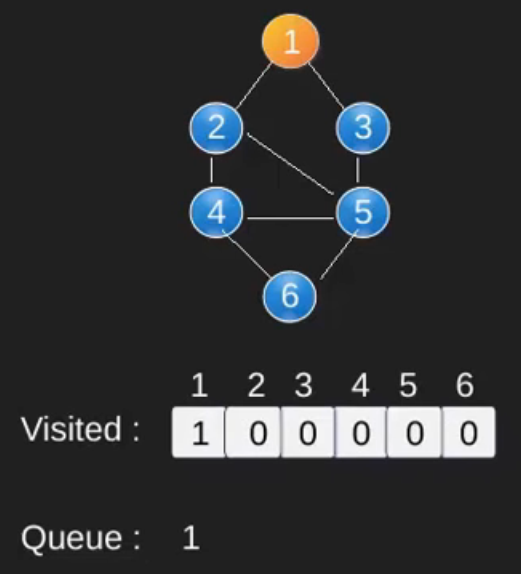
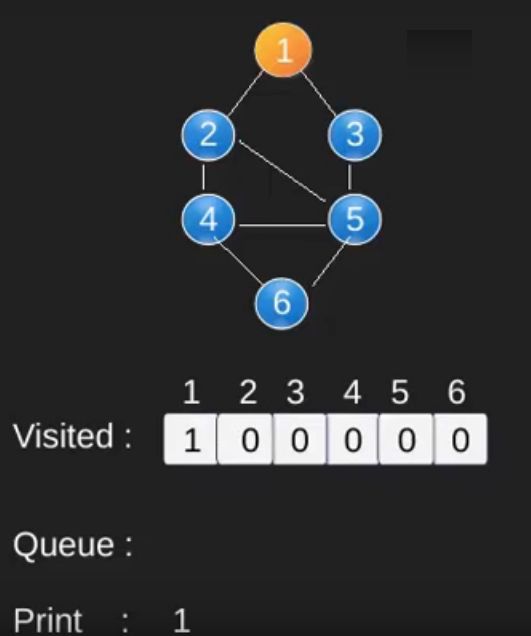
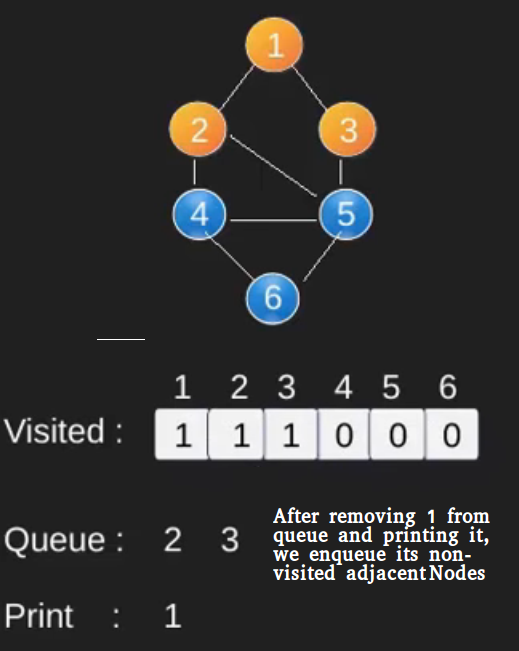
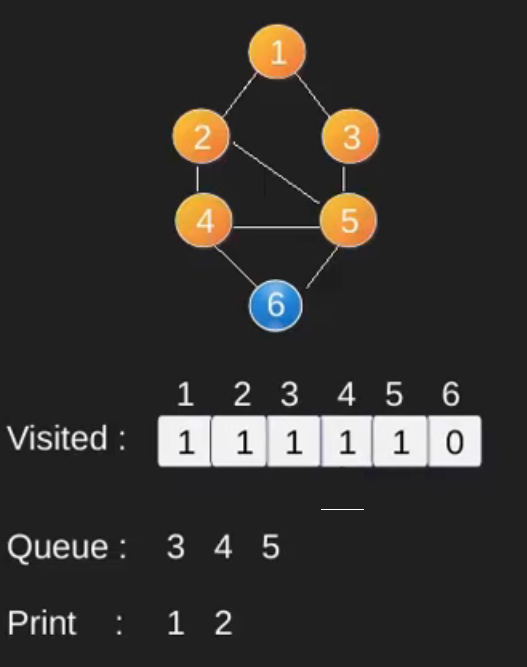
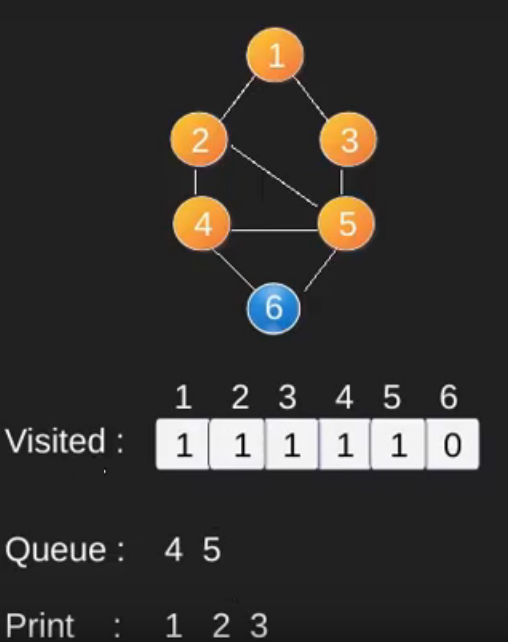
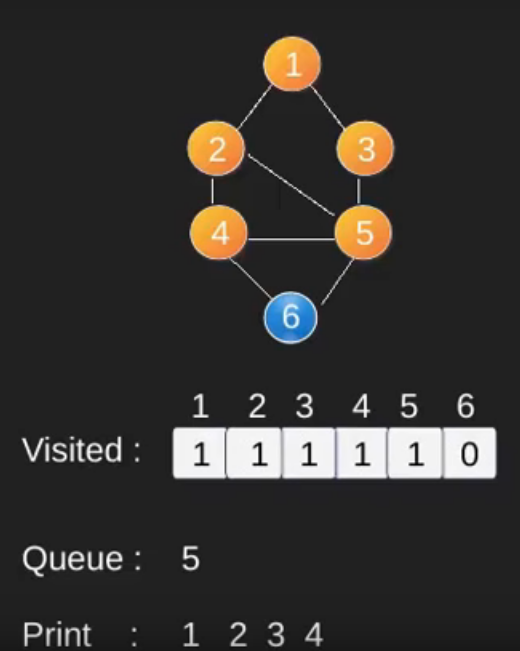
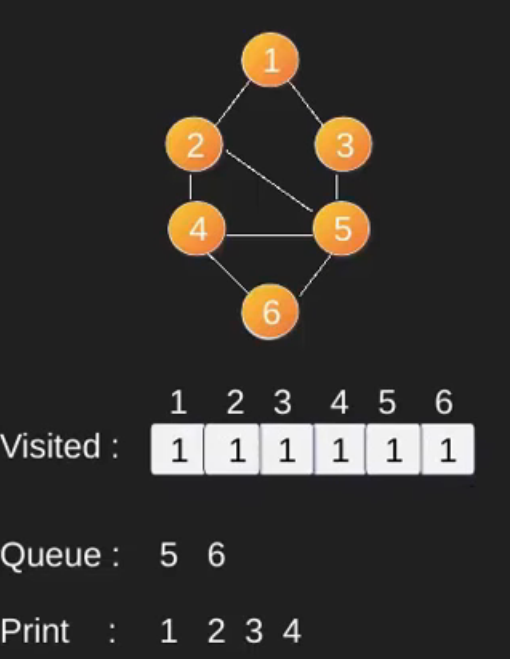
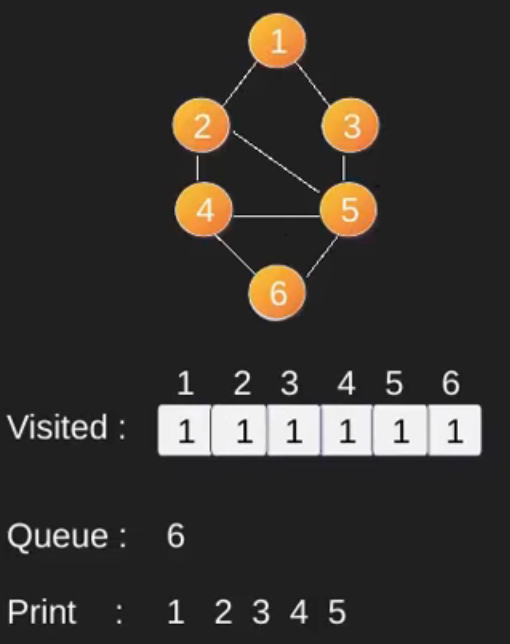
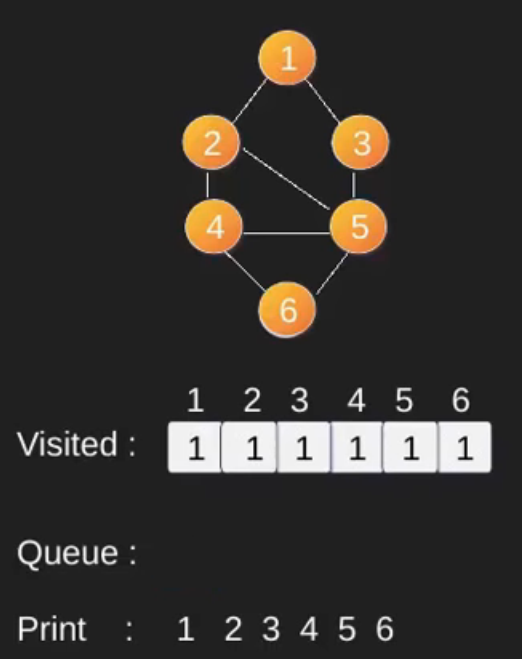
Note that the above code traverses only the vertices reachable from a given source vertex. All the vertices may not be reachable from a given vertex (example Disconnected graph). To print all the vertices, we can modify the BFS function to do traversal starting from all nodes one by one (Like the DFS modified version) .

Time Complexity: O(V+E) where V is number of vertices in the graph and E is number of edges in the graph.